This article was originally prepared for the Self-Service Science Forum around 1997. It has been resurrected and brought into the Wikipedia age to replace all the broken links in the original.

Sir Isaac Newton (1642–1727)

Brief Biography

Despite having an inauspicious schooling and a generally unsociable outlook, Isaac Newton would go on to lead a very successful scientific life. He graduated from Cambridge University (1665) and later achieved his master's degree (1668) and fellowship there. His abilities were well enough known to permit his appointment in 1669 as Lucasian Professor of Mathematics at the University of Cambridge.

His most lasting works were largely the product of two years (1665-67) spent in the English countryside (Woolsthorpe) avoiding the impact of the plague that was ravaging London and Cambridge at the time. His invention of the reflecting telescope during this time earned Newton entry to the Royal Society. It was twenty years (1687), including several years in seclusion refining earlier work, and much encouragement and financial backing from Edmond Halley, before Newton published Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy) and established himself in history.

Newton's contributions picked up from the scientific leads of individuals such as Galileo Galilei, Nicholaus Copernicus, Johannes Kepler, and others to give us advances in the areas of:

• Mathematics (integral and differential calculus or ‘method of fluxions' as he called it)
• Physics of motion
• Gravitation
• Optics (reflecting telescope and the spectrum)

Newton took up the presidency of the Royal Society when he was 61. Queen Anne knighted Newton (c 1705) for services to science and the realm, the first scientist so honoured.

Mental illness and arguments dogged Newton's later life, with notable contemporaries Robert Hooke and Gottfried Leibniz claiming Newton plagiarised their works on attraction between massive bodies and calculus respectively. Newton even delayed publication of his work on optics (Opticks. 1704) until after Hooke's death to avoid confrontation over the nature of light (particle versus wave). The Astronomer Royal, John Flamsteed, was pressured by Newton to publish his catalogue of stars (Newton needed the data to perfect his gravity theory). Flamsteed wanted more time to complete the work. The forced appropriation of the manuscript, court case, and feud lasted ten years and ended with Flamsteed burning the catalogue.

Many tributes followed Newton's death in 1727. One that stands out was made by the great French mathematical astronomer Joseph Louis Lagrange, who said,

Newton was the greatest genius who ever lived, and the most fortunate; for we cannot find more than once a system of the world to establish.

However, Newton said of himself,

If I have seen further than other men, it is because I have stood upon the shoulders of giants.

In poet Alexander Pope's Epitaph for Newton are these lines:

Nature and Nature's laws lay hid in night;
God said, "Let Newton be!" and all was light.

What follows is a brief outline of Newton's legacy.

Calculus

A major leap Newton made at the farm in Woolsthorpe was integral and differential calculus, although he called it the "method of fluxions." Over centuries, many different methods had been devised to do simple things like approximate the area of a surface, or the length or tangent of a curve. Many of these methods were specific to a certain problem. Newton generalised and unified these methods with a straightforward set of processes around 1666. When Newton published his work in 1704, there were accusations regarding plagiarism of the work of Leibniz, who arrived at essentially the same method independently in 1675. Nevertheless, Newton is credited, and these processes have proven themselves invaluable in the fields of mathematics and physics ever since.

Optics

In the time before Newton, all light was thought to be pure white and that passing through glass changed or dimmed the light to produce colours. This was a notion that dated back to the teachings of Aristotle. Newton performed experiments to demonstrate that white light is, in fact, a combination of all the colours that you could see emerging from a prism. The colours Newton saw were described as red, orange, yellow, green, blue, indigo, and violet. Today we know this combination as the visible spectrum. Newton liked the idea of seven colours because they aligned with the seven notes of the musical scale (today we tend to omit indigo). His experiments showed that different colours of light were bent (refraction) by differing amounts as they passed through the glass. Newton chose to try and explain the difference by treating light as particles he called "corpuscles", proposing that the particles of different colours had different masses, thereby explaining the differing degrees of deflection.
Newton, in working with lenses, determined that different colours of light would focus to slightly different locations thereby blurring the image, an effect we now call chromatic aberration . He resolved to avoid this problem by designing a telescope that focussed light using mirrors rather than lenses. The parabolic mirror arrangement he designed is the precursor to the large telescopes of today. They're called Newtonian reflector telescopes.

Laws of Motion

These axioms were first published in Principia.

First Law

Every body continues in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed upon it.

The essence of this statement is that objects will not change speed or direction of travel without a force being applied. In the form of an equation:

Where F is the applied force and a is the resultant acceleration or change in velocity. The resistance to changes in motion is known as inertia and is represented by a quantity called inertial mass.

Second Law

The change of motion is proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed.

A force applied to an object will change the motion (i.e. cause acceleration) of the object in the direction of the force. This law is most often seen as the equation:

Force (F) and acceleration (a) are vectors, that is they contain both magnitude and direction information. The mass (m: the amount of stuff in the object) is used as a measure of the inertia of the object.

Newton explained circular motion in terms of a constant inward acceleration caused by a force that he called centripetal force, and also recognised that there would be an apparent outward force felt by the rotating object (centrifugal force).

Third Law

To every action there is always opposed an equal reaction: or, the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.

If you push an object (apply a force) then an equal and opposite force is applied to you by the object. If you press a stone with your finger, the stone also presses the finger. In equation form:

Gravitation

The legend of Newton and the apple is probably apocryphal. Newton spent substantial time meditating in orchards around the farm in Woolsthorpe, and this is probably the seed of the story.

It was Newton that coined the term gravity (from the Latin gravitas meaning heaviness or weight). His real insight was that the influence of the gravity of Earth could extend all the way to the Moon. This insight, combined with the works of Johannes Kepler, lead to a theory of gravitation that very accurately accounted for the motion of the Moon and the known planets. It also confirmed the Copernican view of a Sun-centred system of planets.

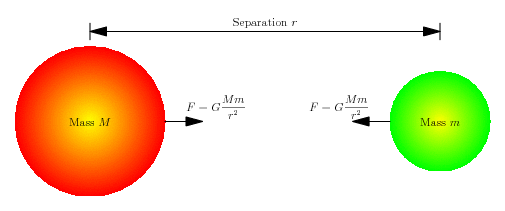
The Newtonian view of gravity is as a force between any pair of objects with mass. The force acts to draw the objects toward each other. The magnitude of the force is given by the equation:

Where G is the Gravitational Constant (\(6.67 \times 10^{-11} \textrm{Nm}^2/\textrm{kg}^2\)), M and m are the gravitational masses of the two objects, and r is the distance between them. (There is an assumption that the inertial mass and gravitational mass of an object were identical).

Universal gravitation allowed the understanding of all sorts of things that previously were inexplicable: Kepler's earlier theory of elliptical planetary orbits, the peculiar motion of comets, tides, free-fall near the Earth, and pendulum motion. It successfully unified work from Copernicus, Galileo, and Kepler into one cohesive theory.

Where It All Stands Today

Today the SI derived unit for force bears Newton's name: Newton or N.

Throughout his work on motion Newton worked on the assumption that both time and space (distance) were absolute. This means that time or length measured by one observer would be measured to have the same values by any other observer. He believed that there was a fixed and unchanging reference against which everything else could be measured. The end of the 19^th^ and the start of the 20^th^ century saw the abandonment of this assumption with confirmation of the invariant and limiting nature of the speed of light, the absence of a detectable ether, and
Albert Einstein's theory of Special Relativity. Time and space are now treated as relative to the observer concerned.

As measurement accuracy improved, discrepancies between orbits predicted using Newton's gravitational theories and reality emerged. One of these was an unexplained shift in the orbit of the planet Mercury around the Sun. Gravitational forces, especially perturbations caused by the presence of other planets, were insufficient to explain this difference, and it wasn't until the formulation of General Relativity that it was better explained. General Relativity also dispensed with the notion of a gravitational force that acted instantaneously by modeling gravity as curvature in space-time.

Notwithstanding the impact of relativity on modern physics, Newton's laws are still taught in high school science classes because they are straightforward and adequate for use in everyday matters.

The 'corpuscular' view of light was a real bone of contention between Newton and those, Hooke included, who insisted on the wavelike nature of light. This century has confirmed that, in a sense, both were correct. Light displays properties of a wave in some circumstances and a particle in others, though it would inaccurate to think of light as either. Quantum mechanics has exposed the world of the photon (light particle) as far weirder than anyone expected in the days of Newton.

Newton's work on the splitting of light, and subsequent work by others, lead to many interesting applications. Today we recognise the spectrum as a continuous range of emissions rather than seven distinct colours. We also recognise that the spectrum of electro-magnetic radiation extends beyond what is visible. This continuous spectrum is affected by the composition of the body emitting the light, and by intervening matter (absorption or Fraunhofer lines). Analysis of light spectra is called spectroscopy. Astronomers use the spectrum of the light from distant objects to determine chemical composition, temperature, absolute magnitude (brightness), velocity, and distance. Spectroscopy is also used in areas like drug testing and chemical analysis.

Further Reading

Newton, Isaac. Philosophiae Naturalis Principia Mathematica 1687. Translated by Andrew Motte 1729. Edited by N. W. Chittenden, 1846.